CIS
LMU, München
Uwe Reichel
Probabilistische Methoden beim Information Retrieval
In der Regel läßt sich eine Anfrage an ein IR-System nicht eindeutig einem bestimmten Informationsbedürfnis zuordnen. Auch ist die ideale Antwort des IR-Systems auf eine Anfrage (nur relevante Dokumente, keine nicht relevanten) unbekannt.
Um mit Unbestimmtheiten wie diesen klarzukommen, bietet sich eine probabilistische Herangehensweise an.
Dazu werden hier zwei Modelle vorgestellt: das klassische BIR-Modell und das Modell von Cooper, et al.
2.1 Unabhängige Ereignisse X1,...,Xn
Sind die Ereignisse X1,...,Xn voneinander unabhängig, so läßt sich die Wahrscheinlichkeit für ihr gemeinsames Auftreten zu folgendem Produkt aufspalten:

Analog gilt für bedingte unabhängige Ereignisse X1,...,Xn|Y:

Herleitung: in einem beliebigen Experiment treten bei insgesamt n Beobachtungen das Ereignis X k mal, das Ereignis Y l mal und beide Ereignisse gemeinsam m mal auf.
Für die entsprechenden Wahrscheinlichkeiten ergibt sich:

Will man nun die Wahrscheinlichkeit von X unter der Bedingung, daß auch Y eintritt, ermitteln, so sind diejenigen m Beobachtungen interessant, bei denen zusätzlich zu Y auch X eingetreten ist und diejenigen l Beobachtungen, bei denen Y überhaupt eingetreten ist. Setzen wir nun diese Häufigkeiten ins Verhältnis und formen den Bruch ein wenig um, ergibt sich die bedingte Wahrscheinlichkeit für X wie folgt:
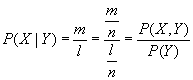
Genauso wie P(X|Y) läßt sich auch P(Y|X) umformen. Teilt man anschließend eine bedingte Wahrscheinlichkeit durch die andere, so erhält man die Gleichung

die direkt zur bayes`schen Formel führt:

Die Quote O(X) ist definiert als Wahrscheinlichkeit eines Ereignisses X geteilt durch die Wahrscheinlichkeit seines Gegenereignisses (Komplementärereignis) ¬X.
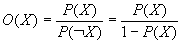
Quote und Wahrscheinlichkeit verhalten sich direkt proportional.
Tritt ein Ereignis mit der Wahrscheinlichkeit 0.5 auf, so ist seine Quote gleich 1.
prinzipielle Frage:
wie hoch ist die Wahrscheinlichkeit Pq(R|d), daß ein gegebenes Dokument d bzgl. einer Anfrage q als relevant R beurteilt wird ?
Ziel ist ein Ranking der Dokumente einer Dokumentensammlung D bezüglich der Wahrscheinlichkeit ihrer Relevanz.
Um diese Wahrscheinlichkeit zu schätzen, werden die Dokumente und Anfragen in Abhängigkeit des IR-Modells durch bestimmte Repräsentationen ersetzt und vereinfachende Annahmen getroffen.
4.1 Grundidee
Bestimme für die in D enthaltenen Terme Gewichte, die etwas darüber aussagen, wie gut die Terme zur Trennung relevanter und nicht relevanter Dokumente bezüglich einer bestimmten Anfrage geeignet sind.
Diese Gewichte werden anhand der Verteilung der Terme in D und - falls vorhanden - unter Einbeziehung von relevance feedback-Daten (Relevanzurteile seitens der Nutzer) berechnet und sagen etwas darüber aus, wie wahrscheinlich die Terme in relevanten Dokumenten auftauchen und wie wahrscheinlich in nicht relevanten.
Summiere dann für jedes Dokument die Gewichte derjenigen Terme auf, die sowohl in der Anfrage als auch im Dokument enthalten sind, und verwende diese Summe als Maß der Relevanz des Dokuments.
Sei T={term1,...,termn} die Menge aller Terme der Dokumentensammlung, dann lassen sich d und q als Vektoren darstellen: d=(t1,...,tn)∈{0,1}n, mit ti=1, wenn termi (1≤i≤n) in d enthalten ist und ti=0, wenn nicht (für q analog).
Pq(R|d) ist aufgrund der Mehrdimensionalität von d unmittelbar kaum zugänglich, da für einen Großteil der möglichen 0-1-Kombinationen zu wenig Beobachtungen vorhanden sind, um verläßliche Werte für die bedingte Wahrscheinlichkeit ermitteln zu können.
Die n-dimensionale Verteilung Pq(R|d) muß also zunächst einmal zerlegt werden.
Hier helfen die oben besprochenen Grundlagen der Wahrscheinlichkeitsrechnung, sprich die bayes`sche Umformung, die Umformung der Wahrscheinlichkeit unabhängiger bedingter Ereignisse und die Definition der Quote, weiter.
Dieses Verfahren wird im Allgemeinen dazu benutzt, eine angenommene a priori-Wahrscheinlichkeit für ein Ereignis in eine durch weitere empirische Daten gestützte a posteriori-Wahrscheinlichkeit überzuführen.
Die a priori-Wahrscheinlichkeit Pq(R), ein zufällig gewähltes Dokument hinsichtlich einer Anfrage als relevant zu beurteilen, wird verbunden mit der a posteriori-Wahrscheinlichkeit Pq(R|d) der Relevanz eines Dokuments gegeben seine beobachteten Eigenschaften.
Beim BIR-Modell sind diese beobachteten Eigenschaften die im Dokument enthaltenen, bzw. nicht enthaltenen Terme aus T, die auch in der Anfrage q vorkommen.
Durch die Verknüpfung von a priori- und a posteriori-Wahrscheinlichkeit läßt sich die Relevanz eines Dokuments gewissermaßen erklären.
Man erhält:
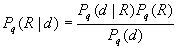
Letztendlich wird (wie später zu sehen ist) bei der Berechnung des Relevanzmaßes für d bezüglich q nur der Faktor Pq(d|R) eine Rolle spielen.
Er gibt die Wahrscheinlichkeit an, mit der ein als relevant beurteiltes Dokument durch den Vektor d charakterisiert ist (also bestimmte Terme enthält und andere nicht).
Mit Hilfe folgender vereinfachender Annahme läßt er sich weiter zerlegen:
in relevanten und in nicht relevanten Dokumenten gelten die gleichen Abhängigkeiten zwischen den Termen aus T. Diese Annahme ist eine Abschwächung der früher verwendeten noch unrealistischeren binary independence assumption, der das BIR-Modell seinen Namen verdankt und derzufolge alle Terme voneinander unabhängig auftreten.
binary independence:
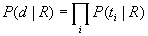
linked dependence:
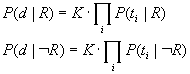
K ist als grobes Maß der linearen Abhängigkeit zwischen den Termen aufzufassen.
In der Herleitung des RSV wird statt P(R|d) die Quote O(R|d) verwendet. Dadurch kürzt sich K wieder raus.
Somit bietet die linked dependence-Annahme, obwohl sie schwächer und damit weniger aus der Luft gegriffen ist als die binary independence-Annahme, den gleichen mathematischen Komfort, nämlich die Aufspaltung einer komplexen Wahrscheinlichkeitsverteilung in seine Komponenten.
(da das Ranking hier stets bzgl. einer bestimmten Anfrage q durchgeführt wird, wird der Index q im Folgenden nicht mehr notiert.)
4.5.1 Herleitung des RSV
gemäß der Bayes´schen Formel läßt sich P(R|d) folgendermaßen umschreiben:
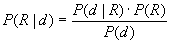
und als Quote:

Unter Ausnutzung der linked dependence Annahme und der Repräsentation von d als Vektor läßt sich die mehrdimensionale Verteilung P(d|R) (genauso wie P(d|¬R)) aufspalten zum Produkt ihrer Komponenten P(ti|R):

Dieses Produkt läßt sich hinsichtlich des Auftretens der Terme aus T in q und d weiter auftrennen:
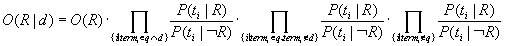
Im zweiten Faktor sind die Terme zusammengefaßt, die sowohl in q als auch in d vorkommen, im dritten Faktor die Terme, die in q, nicht aber in d vorkommen und im vierten Faktor die Terme, die nicht in q vorkommen.
Nimmt man nun weiter an, daß alle Terme, die nicht in q vorkommen, in relevanten Dokumenten genauso wahrscheinlich auftreten wie in nicht relevanten, ist der letzte Faktor gleich 1.
In den anderen Faktoren sind zum einen die Terme der Anfrage, die auch im Dokument d vorkommen, und zum anderen die Terme der Anfrage, die nicht in d vorkommen, zusammengefaßt.
Unter Ausnutzung der Komplementarität der Ereignisse "Vorkommen" und "Nicht Vorkommen" von termi in d erhält man:
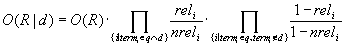
reli steht für P(ti=1|R), nreli für P(ti=1|¬R). Diese Wahrscheinlichkeiten für das Auftreten von termi in relevanten, bzw. nicht relevanten Dokumenten sind die Parameter des BIR-Modells, die es später zu schätzen gilt.
Um aus dem obigen Produkt den Faktor zu isolieren, der in Abhängigkeit des betrachteten Dokuments variiert, fügt man folgenden Faktor (=1) dazu:
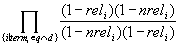
und formt das Produkt um, indem man obigen Ausdruck auf den zweiten und dritten Faktor verteilt:
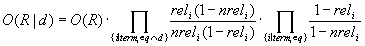
Hier ist nur noch der mittlere Faktor von der Wahl des Dokuments abhängig und damit zur Bildung einer Dokument-Rangfolge bezüglich der geschätzten Relevanz von Interesse.
Um ihn einfacher zu berechnen wird er logarithmiert (Produkte werden so zu Summen), und man erhält den RSV:
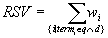
als Summe der Gewichte wi der Terme termi, die sowohl in q als auch in d vorkommen, wobei

Je höher der RSV eines Dokuments, desto wahrscheinlicher ist es bezüglich einer bestimmten Anfrage q relevant. Der RSV ist um so höher,
(1) je mehr Terme ein Dokument mit q gemeinsam hat
(2) je höher die betroffenen Terme gewichtet sind
Das Gewicht wi ist ein Maß dafür, wie gut termi zur Unterscheidung relevanter und nicht relevanter Dokumente bezüglich einer Anfrage q taugt.
Je größer wi, desto wahrscheinlicher taucht termi in einem relevanten Dokument auf und/oder desto unwahrscheinlicher in einem nicht relevanten.
Für jeden termi läßt sich die folgende Kontingenztafel erstellen:
| |
#(relevante Dokumente) |
#(nicht relevante Dokumente) |
#(gesamt) |
| #(Dokumente, die termi enthalten) |
ri |
ni-ri |
ni |
| #(Dok., die terminicht enthalten) |
Q-ri |
(N-Q)-(ni-ri) |
N-ni |
| #(gesamt) |
Q |
N-Q |
N |
hier geben Benutzer des IR-Systems Rückmeldung, für wie relevant sie die für eine bestimmte Anfrage gefundenen (bestgerankten) Dokumente halten.
Zur Initialisierung können die Gewichte wi zum Beispiel gleich der idfi (inverse document frequency) gesetzt werden.

Die Dokumente werden nun entsprechend gerankt und anschließend einem Benutzer zur Beurteilung vorgelegt.
Auf Grundlage der Benutzerurteile werden die Parameter reli und nreli folgendermaßen neu geschätzt.


Bei der Initialisierung werden alle reli gleich einem konstanten Wert (z.B. 0.5) gesetzt
Für die nreli wird angenommen, daß die Verteilung der termi in den nicht relevanten Dokumenten über ihre Verteilung in allen Dokumenten annähernd berechnet werden kann.
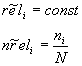
nach dem ersten Ranking auf Grundlage der initialisierten Parameter, werden die höchstbewerteten Dokumente (Schwellwert ist vorher festzulegen) zur Neuschätzung der Parameter herangezogen.
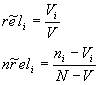
wo Vi gleich der Anzahl der höchstbewerteten Dokumente, die termi enthalten und V gleich der Anzahl aller höchstbewerteten Dokumente.
reli wird hier also über die Verteilung von termi in den höchstbewerteten Dokumenten geschätzt. Für die Schätzung von nreli werden die restlichen Dokumente als nicht relevant betrachtet.
Die folgende Beispiel-Tabelle soll zeigen, wie der RSV eines Dokuments bezüglich einer Anfrage q={t1,...,t6} ermittelt wird.
| |
t1 |
t2 |
t3 |
t4 |
t5 |
t6 |
R |
RSV |
| d1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1.91 |
| d2 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1.91 |
| d3 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1.43 |
| d4 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
2.39 |
| d5 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1.43 |
| d6 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0.48 |
| d7 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1.43 |
| d8 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0.48 |
| ri |
2 |
1 |
3 |
3 |
3 |
2 |
Q=4 |
|
| ni-ri |
1 |
1 |
2 |
1 |
2 |
1 |
N-Q=4 |
Auftreten der Terme t1,...,t6 in den Dokumenten d1,...,d8
R: Beurteilung der Relevanz bzgl. q
N, Q, ni , ri : vgl. Kontingenztafel
exp(wi) : nicht logarithmierter Wert des Gewichts wi des Terms ti
wobei wi=log(reli (1-nreli ) /
(nreli (1-reli )))
Betrachten wir das Dokument d7 genauer:
In diesem Dokument kommen die Terme t1, t2, t3 und t6 aus der Anfrage q vor.
Für diese Terme haben sich im Training folgende Gewichte ergeben:
w1=log3, w2=log1, w3=log3, w6=log3.
Vollziehen wir das für t1 nach:
Die Wahrscheinlichkeiten rel1 und nrel1, also die Wahrscheinlichkeiten, daß t1 in einem relevanten, bzw. nicht relevanten Dokument vorkommt, werden wie oben gesehen folgendermaßen geschätzt:
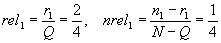
wobei sich die Werte für N, Q, n1 und r1 direkt aus den Trainingsdaten ergeben.
N ist die Gesamtzahl der Dokumente, Q die Anzahl der als relevant beurteilten Dokumente, n1 ist die Gesamtzahl der Dokumente, die t1 enthalten und r1 die Anzahl der als relevant beurteilten Dokumente, die t1 enthalten.
rel1 und nrel1 werden nun folgendermaßen zum Gewicht w1 kombiniert:

Für den RSV für das Dokument d7 müssen nun die Gewichte der Terme, die sowohl in d7 als auch in q vorkommen aufsummiert werden:
RSVd7 = w1+w2+w3+w6 = log3+log1+log3+log3 = 1.43
Das BIR-Modell ist auch in der Lage, RSVs für Dokumente zu liefern, die nicht im Trainingskorpus enthalten waren:
| |
t1 |
t2 |
t3 |
t4 |
t5 |
t6 |
RSV |
| d9 |
1 |
0 |
1 |
1 |
1 |
1 |
2.86 |
hier ergibt sich für d9 folgender RSV:
RSVd9=w1+w3+w4+w5+w6 = log3+log3+log9+log3+log3 = 2.86
Der Lernprozeß des BIR-Modells geschieht in Abhängigkeit von der jeweiligen Anfrage q und von den betrachteten Termen aus T.
Die Werte der Parameter reli und nreli können deshalb zwar auch für nicht im Trainingskorpus enthaltene Dokumente übernommen werden, gelten jedoch nur bzgl. der einen Trainingsanfrage und fehlen für Terme ∉ T.
Das BIR-Modell muß also für jede Anfrage neu trainiert werden.
5.1 Vorbemerkung
In Anbetracht der Einschränkungen des BIR-Modells wäre es wünschenswert, von bestimmten Anfragen, Dokumenten und Termen zu abstrahieren, um eine umfassendere Anwendung eines angelernten probabilistischen Modells möglich zu machen.
Das nun beschriebene von Cooper et al. entwickelte Modell schafft das teilweise.
Dokumente und Anfragen werden nun auf 2 Ebenen repräsentiert. Zum einen durch die Terme Ai (1≤i≤N), die im Training in Dokument und Anfrage gemeinsam aufgetreten sind (match terms) und zum anderen durch Attribute Xj (1≤j≤M) festen Typs dieser Terme.
X1 könnte zum Beispiel die Anzahl von Ai im betrachteten Dokument sein, X2 die Anzahl von Ai in der Anfrage und X3 die idf von Ai.
Es soll eine Beziehung modelliert werden zwischen der Relevanzwahrscheinlichkeit von Dokumenten und deren Eigenschaften, die durch die match-term-Attribute Xj für alle Ai gegeben sind.
Allgemein lassen sich Beziehungen zwischen Variablen mit Hilfe einer Regression beschreiben: abhängige Variablen werden als Funktion von unabhängigen Variablen präsentiert.
Die abhängige Variable ist hier also die Relevanzwahrscheinlichkeit eines Dokuments, und die unabhängigen Variablen sind die Attribute Xj, die für jeden match term Ai einen Wert erhalten.
Da nach dem Training für alle Dokumente im Trainingskorpus bekannt ist, ob sie hinsichtlich einer Anfrage relevant sind oder nicht, kann ihre Relevanzwahrscheinlichkeit nur 2 Werte annehmen: 1 oder 0. Die abhängige Variable Relevanzwahrscheinlichkeit ist also binär.
Ein Funktionstyp, der die Beziehung zwischen unabhängigen und abhängigen binären Variablen einigermaßen widerspiegelt, ist die logistische Funktion auf Grund ihrer sigmoiden Form. Sie ist allgemein durch folgende Formel gegeben:

Für die Wahrscheinlichkeit der Relevanz eines Dokuments bezüglich einer bestimmten Anfrage gegeben der match term Ai, oder anders ausgedrückt: gegeben eine bestimmte Belegung der Variablen X1,...,XM, folgt somit:
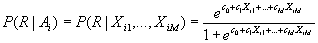
Die Verwendung der Quote O(R|Ai) vereinfacht auch hier vieles. Sie ergibt sich folgendermaßen:

Nimmt man den natürlichen Logarithmus (Umkehrfunktion zu ex) auf beiden Seiten, folgt:

Um die Quote der Relevanz eines Dokuments gegeben seine komplette Repräsentation (also alle Ai) schätzen zu können, muß wieder die linked dependence-Annahme gemacht werden. Es ergibt sich:
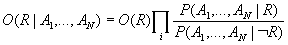
Unter Ausnutzung der Identität:

die folgendermaßen zustandekommt:
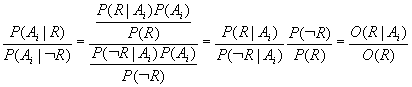
folgt nach Logarithmieren:
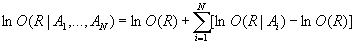
wobei für ln O(R|Ai) bei Anwendung des Modells c0+c1X1+...+cMXM einzusetzen ist.
Der Ausdruck in den eckigen Klammern ist das Gewicht des entsprechenden Terms Ai.
Die Koeffizienten c0,...,cM sind die Parameter dieses Modells.
Um ihre Werte zu ermitteln, müssen die Werte der abhängigen Variable ln O(R|Ai) und die Werte der unabhängigen Variablen Xm direkt aus den Trainingsdaten berechnet und mittels einer Regression miteinander in Beziehung gesetzt werden.
Zur Ermittlung der Koeffizienten werden für alle Dokumente des Trainingskorpus und mehrere Anfragen die Werte für lnO(R|Ai) und Xi1,...,XiM berechnet und in einer Matrix gesammelt.
All diese Werte ergeben sich direkt aus den Trainingsdaten, so für O(R|Ai):

N=Gesamtzahl der Dokumente
Q=Anzahl der relevanten Dokumente
ni=Gesamtzahl der Dokumente, die Ai enthalten
ri=Anzahl der relevanten Dokumente, die Ai enthalten
vgl. Kontingenztafel
Nach Ermittlung der Koeffizienten ergeben sich laut Cooper bessere Schätzwerte für diese Quote als bei dieser Abschätzung direkt aus den Trainingsdaten heraus.
In der Trainingsmatrix umfaßt jedes Dokument-Anfrage-Paar mehrere Zeilen, für jeden match term eine, in die die entsprechenden Werte der abhängigen und unabhängigen Variablen eingetragen werden.
Diese Matrix kann schließlich einer fähigen Statistik-Software übergeben werden, die auf dieser Grundlage die Koeffizienten c0,...,cM berechnet.
Jeder der Koeffizienten ck (k>0) bezieht sich dann auf ein Merkmal X bestimmten Typs. Es müssen also nur M+1 Koeffizienten berechnet werden, und nicht eigene Koeffizienten für jedes Ai.
Dieses Modell ist nach dem Training im Gegensatz zum BIR-Modell nicht auf eine bestimmte Anfrage festgelegt.
Allerdings sind die Koeffizienten ci nur für Eigenschaften der match terms des Trainingskorpus berechnet worden. Bei neuen Anfragen können also für das Ranking nur die Terme verwendet werden, die im Training mindestens einmal als match term aufgetreten sind.
Auch eine Vergrößerung der Dokumentensammlung kann zu Verzerrungen führen, wenn sich Eigenschaften Xj der match terms auf den gesamten Korpus beziehen.
Dieser Einschränkung kann man aber begegnen, indem man das Modell in der Anwendungsphase weiterlernen läßt.
Literatur:
Ferber, R. (1995). Data mining und Information Retrieval (Zugriff derzeit verboten)
Fuhr, N. (1993). Information Retrieval: Skriptum zur Vorlesung
Greengrass, E. (2000). Information Retrieval: A Survey
Yaeza-Bates, R., Ribeiro-Neto, B. Modern Information Retrieval. Acm Press Series.
![]()
![]()
![]()
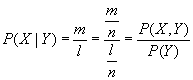

![]()
![]()
![]()
![]()
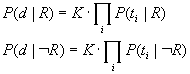
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
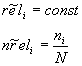
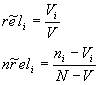
![]()


![]()

![]()
![]()
![]()
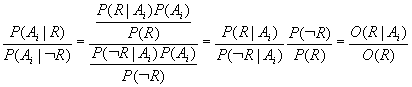
![]()
