Grundlagen

Die naheliegendste Methode, etwas zu finden, besteht in einem Abgleich zwischen der Anfrage und der zur Verfügung stehenden Datenbasis. Bei der Anfrage kann es sich z. B. um ein Kochbuch handeln, und bei der Datenbasis um einen Buchladen. Ein Mensch wird auch einen Titel wie "Indische Leckerbissen" in Betracht ziehen, während eine Anfrage in einer Suchmaschine nur die Titel zurückliefern wird, in denen das Wort "Kochbuch" vorkommt. Dadurch entgehen uns aber sehr viele interessante Titel.

Suchmaschinen, die auf der Basis von lexikalischer Übereinstimmung arbeiten, lassen gängige Phänomene wie Synonymie bzw. Polysemie ganz außer Acht, d.h. dass Artikel, die relevent sind aber nicht ganz genau die angegebenen Suchbegriffe enthalten nicht ermittelt werden, und dass auch völlig uninteressante Artikel als Antwort auf die gestellte Anfrage ermittelt werden. Eine Anfrage nach "Auto" würde z. B. keine Dokumente über Wagen ode LKW zurückliefern, während eine Anfrage der Art "Band Buch" uns wahrscheinlich auch Dokumente mit Büchern über Musikbands zurückliefern würde.

Die hier vorgestellte Methode (LSI = Latent Semantic Indexing) versucht mittels statistischer Indizes mit diesen Problemen fertig zu werden. LSI geht davon aus, dass den verschiedenen Wörtern eine Art latente bzw. immanente Struktur zugrunde liegt, die z. B. durch die Auswahl unterschiedlicher Wörter, um das Gleiche zu bezeichnen (Synonymie), "verdunkelt" wird. Diese immanente Semantik versucht LSI wieder ans Licht zu bringen.

 

Voraussetzungen

Zweck dieses Referats ist es zwar nur einen Einblick in die LSI-Methode zu gewähren und nicht sie bis ins kleinste Detail zu erläutern. Trotzdem werden für das Verständnis dieses Textes ein paar wenige Grundkenntnisse über lineare Algebra notwendig sein.

Diejenigen, die mit den Grundlagen der Matrizenrechnung vertraut sind, können gleich mit dem nächsten Abschnitt anfangen. Alle anderen verweisen wir auf folgende Einführungen:

Einführung in die Matrizenrechnung

Grundlagen der Matrizenrechnung

Kurzer Einblick in Eigenwert/Eigenvektor

 

Einführung

Wir betrachten eine Matrix $A$ $(m \times n)$, die aus $m$ Reihen und $n$ Spalten besteht. Die Reihen $i=1$ bis $i=m$ stehen für die Terme $Term_1,\ldots, Term_m$, die Spalten $j=1$ bis $j=n$ stehen für die Dokumente $Dok_1,\ldots, Dok_n$. In die Kästen wird eingetragen, wie oft der Term $i$ im Dokument $j$ vorkommt.

 

Matrix $A$ :

	Dok 1	Dok 2	...	Dok n
Term 1	1	1	...	0
Term 2	0	1	...	0
Term 3	0	0	...	1
...	...	...	...	...
Term m	0	1	...	0

 

Matrix$A$ (Transponierte von der Matrix $A$ )

	Term 1	Term 2	Term 3	...	Term m
Dok 1	1	0	0	...	0
Dok 2	1	1	0	...	1
...	...	...	...	...	...
Dok n	0	0	1	...	0

Zur Veranschaulichung nehmen wir an, dass wir folgende Datenbank zur Verfügung haben:

Label	Titles
D1	A Course on Integral Equations
D2	Attractors for Semigroups and Evolution Equations
D3	Automatic Differentiation of Algorithms Theory, Implementation, and Application
D4	Geometrical Aspects of Partial Differential Equations
D5	Ideals, Varieties, and Algorithms – An Introduction to Computational Algebraic Geometry and Commutative Algebra
D6	Introduction to Hamiltonian Dynamical Systems and the N-Body Problem
D7	Knapsack Problems: Algorithms and Computer Implementations
D8	Methods of Solving Singular Systems of Ordinary Differential Equations
D9	Nonlinear Systems
D10	Ordinary Differential Equations
D11	Oscillation Theory for Neutral Differential Equations with Delay
D12	Oscillation Theory of Delay Differential Equations
D13	Pseudodifferential Operators and Nonlinear Partial Differential Equations
D14	Sinc Methods for Quadrature and Differential Equations
D15	Stability of Stochastic Differential Equations with Respect to Semi-Martingales
D16	The Boundary Integral Approach to Static and Dynamic Contact Problems
D17	The Double Mellin-Barnes Integrals and Their Applications to Convolution Theory

Die unterstrichenen Wörter stellen die Schlüsselwörter dar. Das Auswahlkriterium war, dass sie mindestens zwei Mal in der Datenbasis vorkommen müssen, wobei die sog. Stoppwörter davon ausgenommen wurden: a, and, for, the, etc.

Diese Information können wir auch in einer Matrix darstellen, indem wir in die entsprechenden Zellen $(i, j)$ die Häufigkeit des Wortes (=Term) $i$ im Dokument $j$ eintragen:

16 x 17 Termen-Dokumenten-Matrix $A$

Terme	Dokumente
	d1	d2	d3	d4	d5	d6	d7	d8	d9	d10	d11	d12	d13	d14	d15	d16	d17
algorithms	0	0	1	0	1	0	1	0	0	0	0	0	0	0	0	0	0
application	0	0	1	0	0	0	1	0	0	0	0	0	0	0	0	0	0
delay	0	0	0	0	0	0	0	0	0	0	1	1	0	0	0	0	0
differential	0	0	0	1	0	0	0	1	0	1	1	1	1	1	1	0	0
equations	1	1	0	1	0	0	0	1	0	1	1	1	1	1	1	0	0
implementation	0	0	1	0	0	0	1	0	0	0	0	0	0	0	0	0	0
integral	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1
introduction	0	0	0	0	1	1	0	0	0	0	0	0	0	0	0	0	0
methods	0	0	0	0	0	0	0	1	0	0	0	0	0	1	0	0	0
nonlinear	0	0	0	0	0	0	0	0	1	0	0	0	1	0	0	0	0
ordinary	0	0	0	0	0	0	0	1	0	1	0	0	0	0	0	0	0
oscillation	0	0	0	0	0	0	0	0	0	0	1	1	0	0	0	0	0
partial	0	0	0	1	0	0	0	0	0	0	0	0	1	0	0	0	0
problem	0	0	0	0	0	1	1	0	0	0	0	0	0	0	0	1	0
system	0	0	0	0	0	1	0	1	1	0	0	0	0	0	0	0	0
theory	0	0	1	0	0	0	0	0	0	0	1	1	0	0	0	0	1

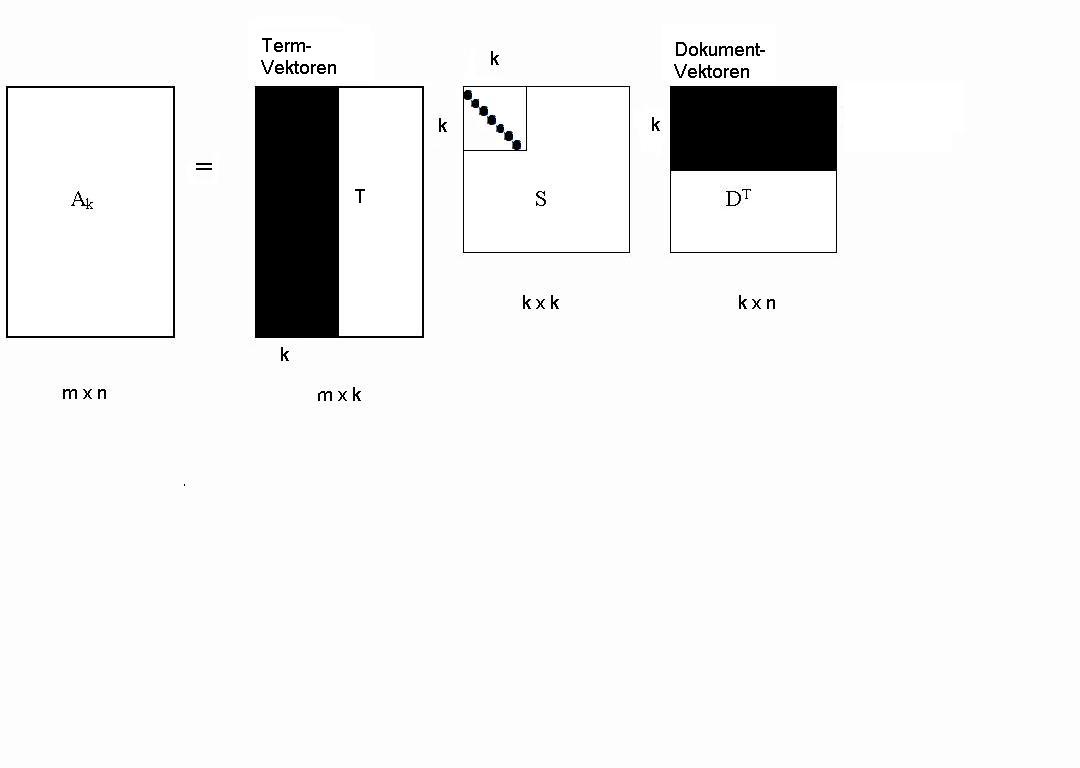
Nach der Methode der Singulärwertzerlegung können wir die Matrix $A$ in folgende Faktoren zerlegen (näheres dazu kann man unter Singulärwertzerlegung von Ingo H. de Boer nachlesen):

$$A = T_0S_0D_0^T,$$

wobei $T_0$ die Matrix mit den Eigenvektoren von $AA^T$ $(m \times r)$, $D_0$ die Matrix mit den Eigenvektoren von $A^TA$ $(r\times n)$ und $S_0$ die Diagonalmatrix mit den quadratischen Wurzeln der Eigenwerte von $AA^T$ $(r\times r)$ sind. $r$ steht für den Rang der Matrix $AA^T$ bzw. $A^TA$.


Warum multipliziert man die Matrix $A$ mit ihrer Transponierten?

Um diese Frage zu beantworten, müssen wir uns vorher in Erinnerung rufen, wie zwei Matrizen multipliziert werden: In die Zelle $(i, j)$ wird das Skalarprodukt der $i$-ten Reihe der ersten Matrix mit der $j$-ten Spalte der zweiten Matrix eingetragen.

In unserem Fall heißt das, dass wir mit der Matrix $AA^T$ eine Sammlung (= die Werte in den Zellen) von Ähnlichkeitsmaßen zwischen den verschiedenen Termen haben, während in den Zellen der Matrix $A^TA$ Ähnlichkeitsmaße zwischen den Dokumente eingetragen sind.

Warum berechnet man die Eigenvektoren?

Die Eigenvektoren sind linearunabhängig, d. h. dass keiner von ihnen als lineare Kombination der anderen darstellbar ist. Zwei Vektoren sind linear abhängig, wenn sie parallel sind: der eine Vektor kann mittels Multiplikation mit einem Faktor lambda aus dem anderen berrechnet werden. Für uns bedeutet linear unabhängig, dass Informationen nicht redundant dargestellt sind.

In der Diagonalmatrix $S_0$ werden also die errechneten Eigenwerte der Größe nach angeordnet. Die $k$ größten Werte werden beibehalten, und die restlichen werden gleich Null gesetzt. Somit kann man auch die entsprechende Anzahl von Spalten bzw. Reihen bei $T_0$ bzw. $D_0$ löschen.

Der Wert von $k$ wird empirisch ermittelt. Er soll groß genug sein, um einerseits die Charakteristika der behandelten Daten beizubehalten, und andererseits klein genug, um mögliche Fehler und unwichtige Daten herauszufiltern.

$$A_k = T_kS_kD_k^T$$